Know About Binary Search Tree
Table of contents
- Introduction
- Special Property in BST: Inorder Traversal Yields a Sorted Sequence
- Searching Technique in BST
- Key Takeaways:
- Searching Time Complexity in BST
- Types of Binary Trees
- Build a BST from Array
- Deleting a Node in BST
- Deletion Logic
- Case 2: Node with One Child (1 child)
- Case 3: Deleting a Node with 2 Child Nodes
- Inorder Successor →
- Using Inorder Successor in Deletion:
Introduction

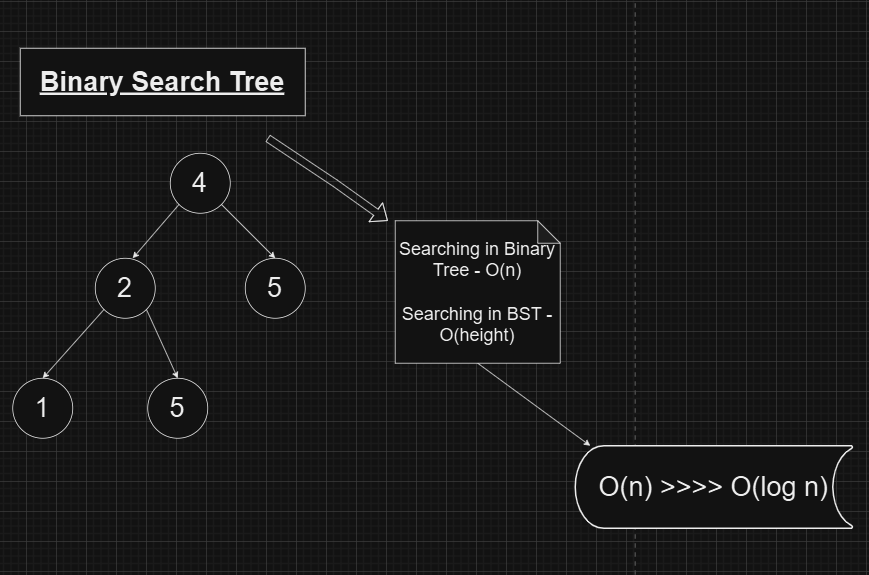
Binary Search Trees (BSTs) are a specialized form of binary trees designed to optimize the searching process. While a standard binary tree offers no inherent structure to facilitate faster lookups, BSTs introduce a pivotal property: for every node, all elements in its left subtree are smaller, and all elements in its right subtree are larger. This ordered structure enables BSTs to significantly enhance search efficiency.
In a regular binary tree, the search operation has a time complexity of O(n) in the worst case. This is because, without any specific order, the algorithm may need to traverse each of the n nodes to locate a desired element. However, BSTs reduce this complexity to O(h), where h is the height of the tree. For balanced trees, the height h approximates logn, leading to an average-case search complexity of Θ(logn). This improvement is substantial, as O(logn) is significantly smaller than O(n), particularly for large datasets.
The practical utility of BSTs can be seen in scenarios where efficient and repeated search operations are crucial. For example, many companies employ BSTs to construct lookup tables or manage structured data that requires frequent searches. By leveraging BSTs, these operations become faster and more efficient, making them ideal for applications requiring optimal performance.
Special Property in BST: Inorder Traversal Yields a Sorted Sequence
One of the most significant properties of a Binary Search Tree is that an inorder traversal of the tree produces a sorted sequence of its nodes. This property stems directly from the fundamental arrangement of BSTs: for every node, all elements in the left subtree are smaller, and all elements in the right subtree are larger.
What does this mean?
When you perform an inorder traversal — visiting the left subtree, the current node, and then the right subtree recursively — the nodes are accessed in ascending order. This behavior makes BSTs particularly useful for applications where sorting or ordered retrieval is required.

For example, if you are given an unsorted dataset and need to retrieve its elements in ascending order repeatedly, inserting the data into a BST and then performing an inorder traversal is an efficient solution.
This property is so central to BSTs that it often serves as the first step in solving many BST-related problems, such as validating if a tree is a BST, finding the kth smallest element, or performing range queries efficiently.

Searching Technique in BST
BSTs provide a far more efficient searching mechanism than standard Binary Trees, primarily due to their unique properties and reduced time complexity. Let’s explore why this is the case.
Validating a BST
Before diving into the searching process, let’s briefly recap the fundamental property of a BST:
Every node in the left subtree of a parent node must have a value less than the parent node.
Every node in the right subtree must have a value greater than the parent node.
If any node violates this property, the structure cannot be considered a valid BST.
For example, suppose we need to search for a key 7 in a given BST. Before understanding how BST optimizes the search, consider the scenario where this tree is treated as a regular binary tree. Searching in a binary tree would involve:
Comparing the root node’s value with the search key. If it matches, return the node.
If not, recursively searching in the left subtree.
If not found in the left subtree, searching in the right subtree.
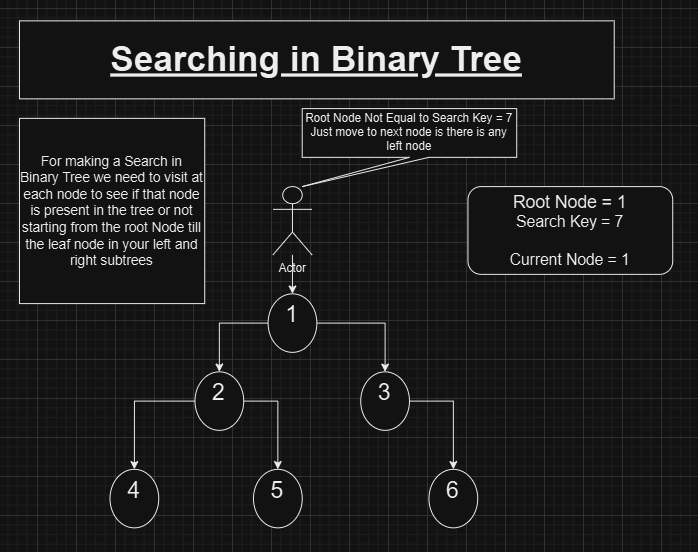

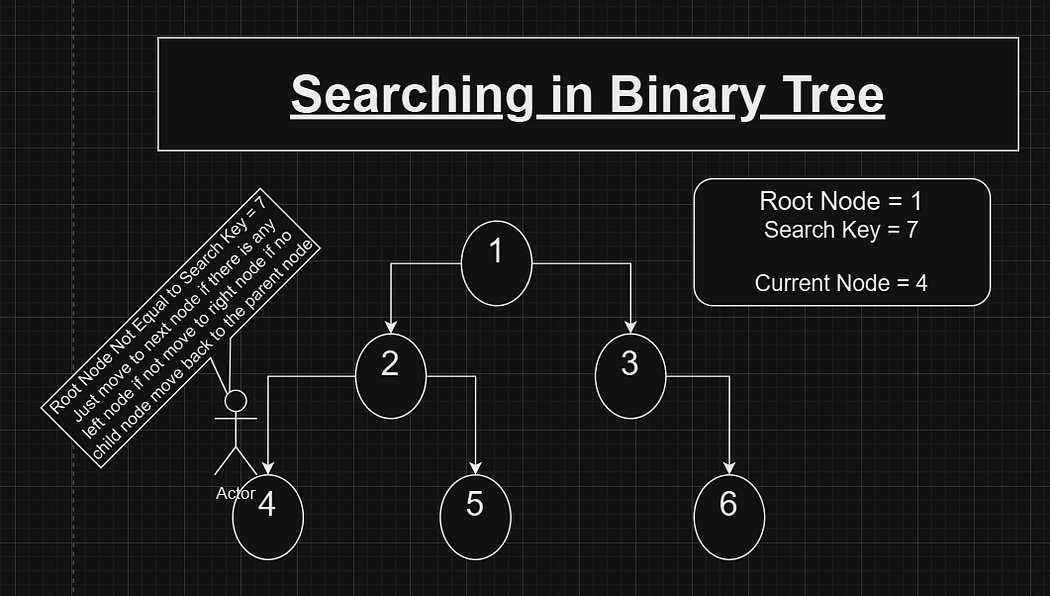
Like this we will keep on moving to each node till the key is found . In the worst-case scenario, this approach requires checking every node in the tree. For n nodes, this results in a time complexity of O(n).
Optimized Search in BST
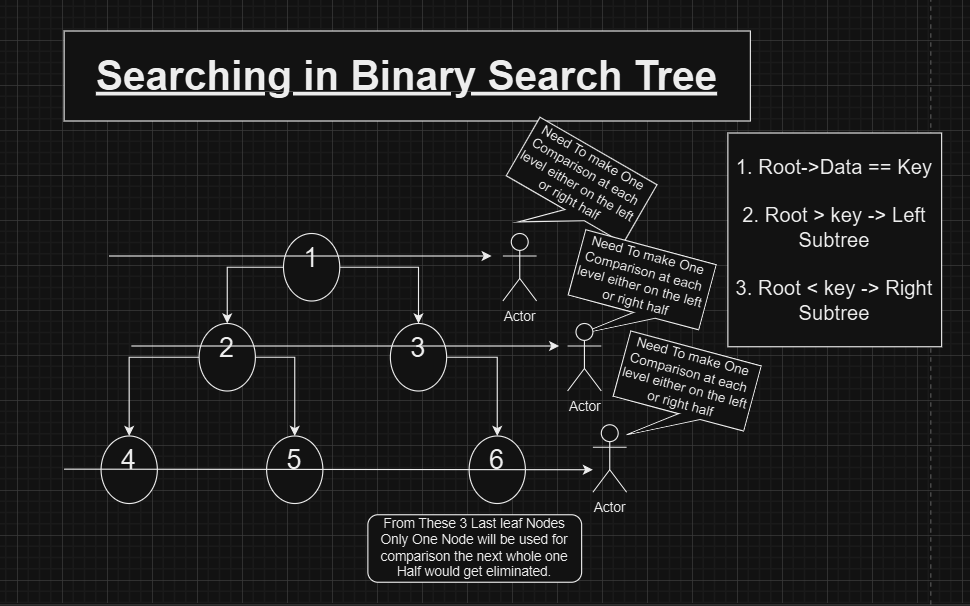
BSTs leverage their special property — ordered nodes in the left and right subtrees — to reduce the search complexity to O(logn) in the average case. This property allows the application of a binary search-like logic in BSTs.
Here’s how the search mechanism works:
- Compare the root node’s value with the search key:
- If it matches, return the node.
If the search key is less than the root’s value, search in the left subtree.
If the search key is greater than the root’s value, search in the right subtree.
Unlike a binary tree, where both subtrees may need to be checked, BSTs allow us to eliminate half of the tree at each level of comparison.
Binary Search and BST
Binary Search, applied on sorted arrays or vectors, works by dividing the search space in half at each step. A mid-point is selected, and the search key is compared to the value at that point:
If the search key matches the mid-point value, return the index.
If the search key is greater, narrow the search to the right half.
If the search key is smaller, search in the left half.
This concept parallels the BST search process. Consider the root of a BST as the “mid-point” of the tree:
Moving to the left subtree is akin to searching the left half of an array.
Moving to the right subtree mirrors searching the right half.
Each node in a BST satisfies the property that its left subtree contains smaller values and its right subtree contains larger values, ensuring this logic applies recursively throughout the tree.
Comparison with Binary Trees
In a normal binary tree, search operations may require examining all nodes, resulting in O(n) complexity. This is because both left and right subtrees must be explored when the search key isn’t found at a node.
In contrast, a BST reduces the search space at every level, focusing on only one subtree — left or right — based on the comparison. Thus, in a balanced BST, the height of the tree is approximately logn, making the search complexity O(logn).
Key Takeaways:
BST search is efficient due to its ordered structure, resembling binary search logic.
Each level of the tree requires comparing the search key with only one node.
In the average case, this reduces search complexity from O(n) in binary trees to O(logn) in BSTs.

Searching Time Complexity in BST
In a Binary Search Tree (BST), the search operation is efficient because we compare only one node at each level of the tree. The total number of levels in a BST determines its height, and the search time complexity is directly related to this height.
Time Complexity:
The time complexity of searching in a BST is O(height), as the number of comparisons required is equal to the height of the tree.
In an average case, for a balanced BST, the height is approximately logn, leading to a search complexity of O(logn).
However, in the worst case, such as in a skewed BST, the height equals the number of nodes (n), resulting in a search complexity of O(n).

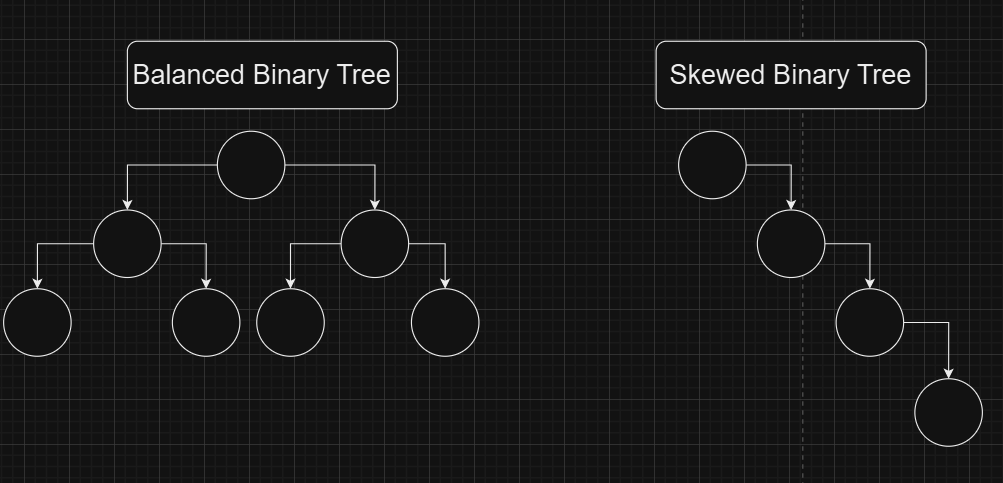
Types of Binary Trees
The height of a BST is influenced by its structure, which can take different forms:
- Balanced Binary Tree:
A balanced binary tree maintains a nearly equal number of nodes in its left and right subtrees at every level.
This ensures the height of the tree remains approximately logn, enabling efficient search operations with a time complexity of O(logn).
Balanced BST variants, such as AVL Trees and Red-Black Trees, are designed specifically to maintain balance.
2. Skewed Binary Tree:
A skewed tree occurs when all nodes are arranged in a single path, either to the left or the right.
In this case, the tree’s height equals the number of nodes (n), degrading the search time complexity to O(n).
Skewed trees are typically a result of inserting nodes in sorted order without balancing mechanisms
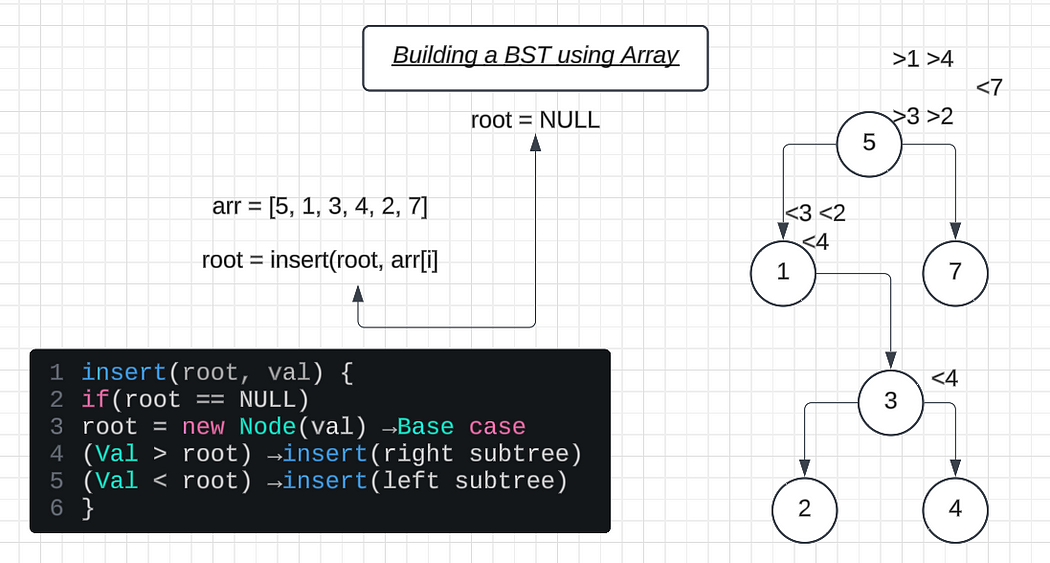
Build a BST from Array
Building a Binary Search Tree (BST) is similar to building a Binary Tree but incorporates the logic of the binary search technique to maintain the BST property.
To create a BST node, we follow the standard process for building nodes in a Binary Tree. However, this time we ensure that each node is attached to the correct position in the tree, guided by the BST property.
Steps to Build a BST
Node Creation:
Each node in the BST is created like a standard Binary Tree node, with pointers to its left and right children.Finding the Correct Position:
Unlike a Binary Tree, where nodes can be inserted sequentially, a BST requires finding the correct position for the new node based on its value:
- If the value to be inserted is less than the root’s value, the node is placed in the left subtree.
- If the value to be inserted is greater than the root’s value, the node is placed in the right subtree.Insertion Logic:
The node will be inserted at the first position where aNULLvalue is encountered. Therefore, the base case is simple:
- If
root == NULL, create a new node at that position.
Before inserting a node, we must determine its correct position in the BST:
If the value to be inserted is less than the root’s value, it will go into the left subtree.
If the value is greater than the root’s value, it will go into the right subtree.
In the insert function, we pass the root and the value to find the right spot recursively.
#include<iostream>
using namespace std;
class Node {
public:
int data;
Node* left;
Node* right;
Node(int value) {
this->data = value;
this->left = this->right = NULL;
}
};
/**
* A recursive insert function for adding the Node in the BST.
*/
Node* insert(Node* root, int value) { //Time Complexity of Insert function is O(log n). For inserting a single Node
//Base case: If the root is NULL then this means we need to create a new node and return the value of the root only.
if(root == NULL) return root = new Node(value);
//Self-work: If the root is not NULL and a value is passed to us then we need to first find out the correct position for that value to be inserted in the BST.
//In short we have to search for the appropiate position and where we will find the appropiate position there it will have a NULL value and the node will be inserted at that position.
if(value < root->data) root-> left = insert(root->left, value); //Left subtree case.
else root->right = insert(root->right, value); //Right Subtree case.
//The value can be either lesser or greater then the root node. They value cann't be equal to root node as BST has unique values in it.
return root;
}
/**
* This buildBST function takes an array of values and a builds a BST out of the values given.
* And at the end returns the root of the BST at the end of the function. That's why its return type is Node*.
* n here is the size of the array.
*/
Node* buildBST(int arr[], int n) { //Time complexity will be O(n log n) not exactly because each time the size of the tree is changing.
//What buildBSt does is it tries to travel one by one each value of the array and tries to build the node.
//STEP 1: At starting we have created a root with the value NULL in it.
Node* root = NULL;
for(int i=0; i<n; i++) {
//STEP 2: Is running a loop which will traverse the value of BST one by one.
root = insert(root, arr[i]); //This insert function will insert the node at its correct position and return us the new root value which we will just update in the root variable.
}
//STEP 3: And finally just returning our root Node.
return root;
}
void inorder(Node* root) {
if(root == NULL) return;
inorder(root->left);
cout<<root->data<<" ";
inorder(root->right);
return;
}
int main() {
int arr[] = {5, 1, 3, 4, 2, 7};
Node* root = buildBST(arr, 6); //This function will return us the root value of the BST Tree.
inorder(root);
return 0;
}
#include<iostream>
using namespace std;
class Node {
public:
int data;
Node* left;
Node* right;
Node(int value) {
this->data = value;
this->left = this->right = NULL;
}
};
bool searchBST(Node* root, int &searchKey) { //Time Complexity -> O(height)
//Base case: If we are on the leaf node or the tree is empty in that case, it will return a false.
if(root == NULL) return false;
//Self-work: If the root is only the search key return true.
if(root->data == searchKey) return true;
//Assumption: If root isn't the search key then find it in either of the two sides depending upon the search key value.
if(searchKey < root->data) searchBST(root->left, searchKey);
else searchBST(root->right, searchKey);
}
Node* insert(Node* root, int value) {
if(root == NULL) return root = new Node(value);
if(value < root->data) root->left = insert(root->left, value);
else root->right = insert(root->right, value);
return root;
}
Node* buildBST(int arr[], int n) {
Node* root = NULL;
for(int i=0; i<n; i++) {
root = insert(root, arr[i]);
}
return root;
}
int main() {
int arr[] = {5, 1, 3, 4, 2, 7};
Node* root = buildBST(arr, 6);
int searchKey = 9;
bool ans = searchBST(root, searchKey);
cout<<ans<<" ";
return 0;
}
Deleting a Node in BST
In this section, we will see how to delete a node in a BST. Before deleting a node, we need to first check which type of node it is. Based on the type, we can encounter three different cases for deletion:
Deleting a Leaf Node (0 children):
If the node doesn’t have any child nodes, it is called a leaf node. Deleting a leaf node is very simple. we can just replace it with aNULLvalue, indicating that the node has been removed.Deleting a Node with One Child (1 child):
If the node to be deleted has only one child, we cannot replace it with aNULLvalue, as doing so would disconnect the subtree below it. In this case, we need to link the parent of the deleting node to its child.Deleting a Node with Two Children (2 children):
If the node has both left and right child nodes, the deletion process becomes a bit tricky. We need to carefully arrange the left and right subtrees of the deleting node to maintain the BST properties.
Before performing any deletion, the first step is to locate the node we want to delete. Depending on the case, we then delete the node.
To implement this, we can create a deleteNode function that returns the updated root node of the tree after deletion. The function takes the root node and the value to be deleted as arguments.
Deletion Logic
Base Case:
If the tree is empty, there’s nothing to delete:
if (root == NULL) return NULL;Finding the Node to Delete:
If the value to delete equals the root node’s value, we proceed to delete the node.
If the value to delete is less than the root node’s value, search for the node in the left subtree:
root->left = deleteNode(root->left, value);If the value to delete is greater than the root node’s value, search for the node in the right subtree:
root->right = deleteNode(root->right, value);
Once the node to delete is found, the following cases are handled:
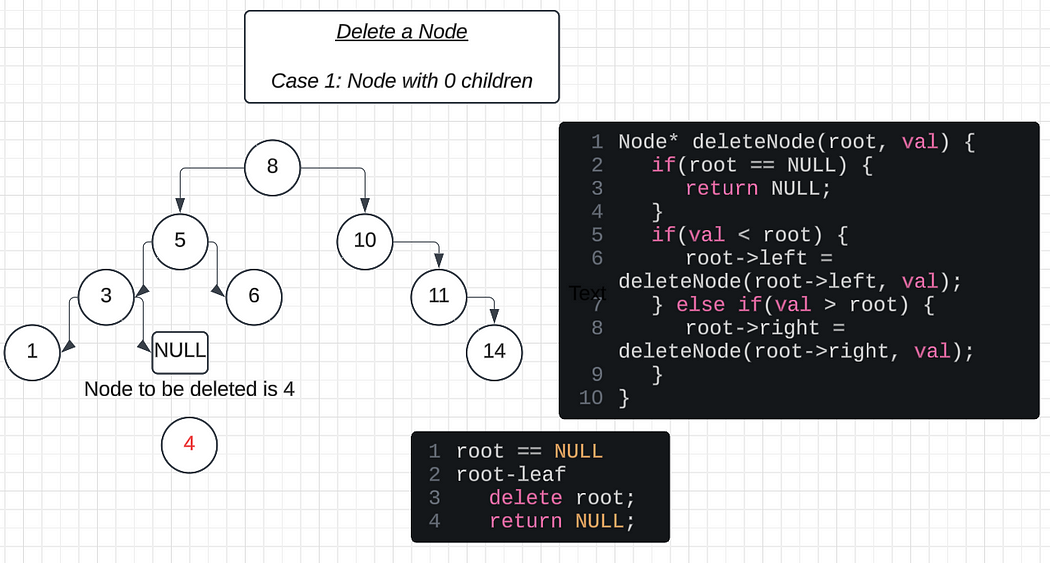
Case 1: Leaf Node (0 children)
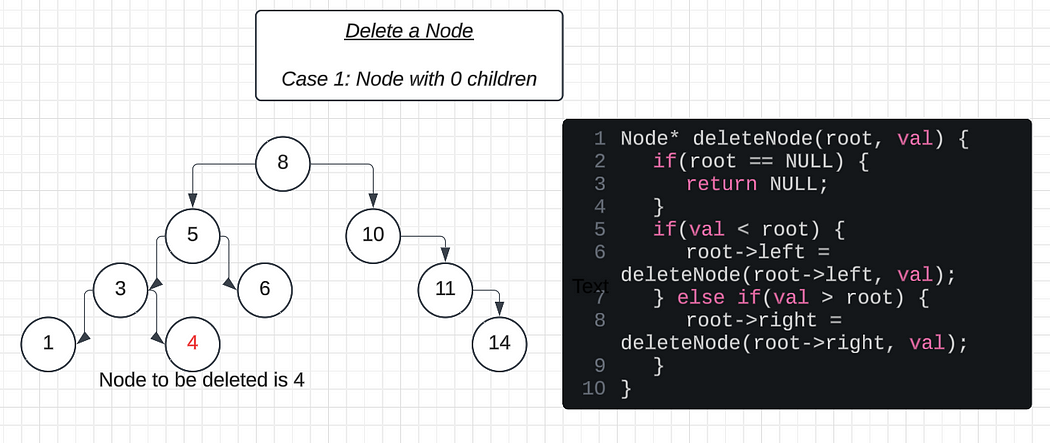
Check if the node is a leaf node:
- Bothroot->leftandroot->rightareNULL.If it is a leaf node, replace it with a
NULLvalue to indicate its deletion.Return
NULLto the parent node, which will automatically detach the node from the tree.Free the memory allocated to the node using the
deletekeyword.
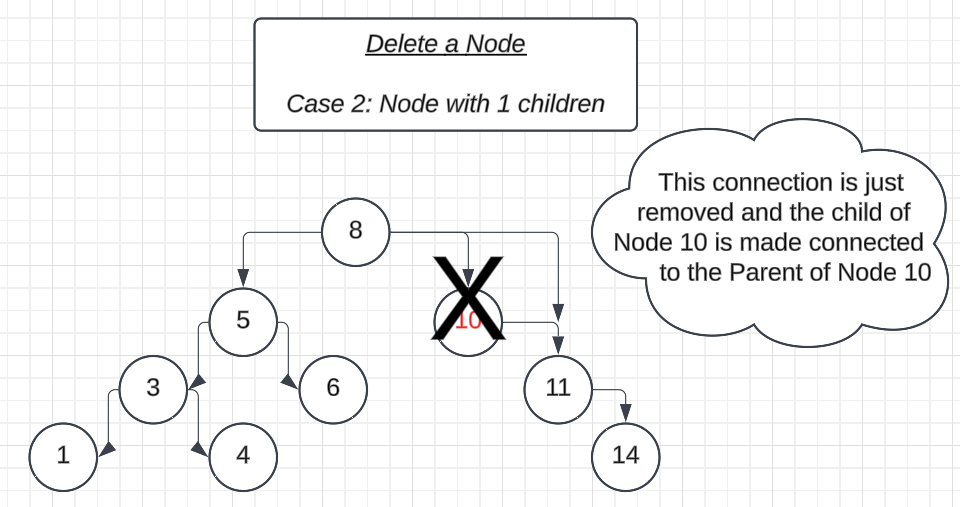
Case 2: Node with One Child (1 child)
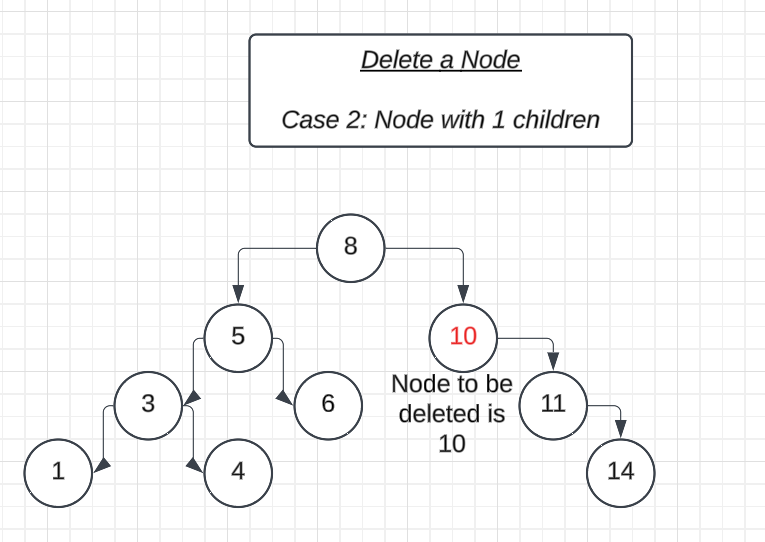
- Check if the node has only one child:
- One of
root->leftorroot->rightisNULL, while the other has a valid Node value attached to it.
2. Link the parent of the deleting node directly to its child:
If the left child exists, return
root->left.If the right child exists, return
root->right
3. This effectively bypasses the deleting node, maintaining the tree structure.
4. Free the memory of the deleted node using the delete keyword.
Case 3: Deleting a Node with 2 Child Nodes
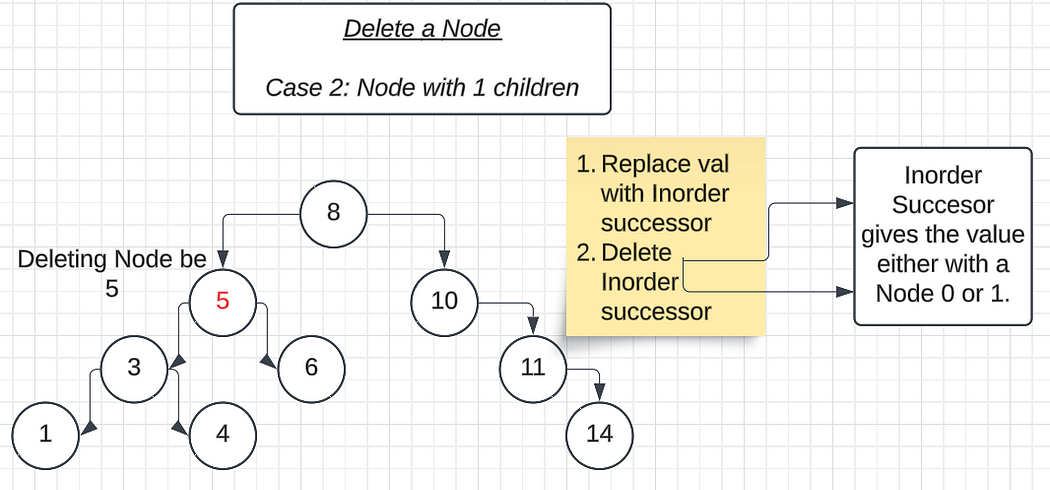
In this case, once we find the root node we want to delete and are standing on it, the next step is to check if it has child nodes.
Here, the node has both left and right child nodes, making the process slightly more complex.
We need to carefully arrange its left and right subtrees since we cannot randomly attach the parent node to one of the child nodes. This is because both left and right subtrees have valid values that need to maintain the BST property.
There is a standard method or logic to handle the deletion of a node with two child nodes:
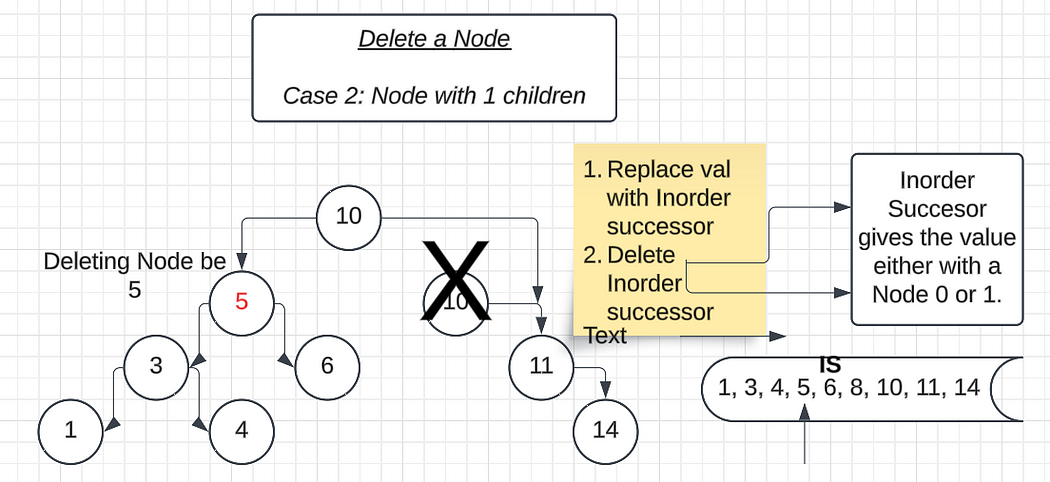
1. First, replace the value of the node to be deleted with its inorder successor (the smallest value in the right subtree).
2. Next, delete the inorder successor node from the tree.
- Fun fact: The inorder successor will always have either 0 or 1 child node, making its deletion easier. The logic for handling 0 or 1 child node cases has already been explained in the earlier sections.
Inorder Successor →
Let’s first talk about how we can find the Inorder Successor in any BST. Let’s assume we are given a valid BST and want to find the Inorder Successor of the root node. The Inorder Successor of the root node will be the node greater than the root node since we are looking for the “next” node in sequence, which means it will be the smallest node greater than the root node.
Now, we know that the Inorder Successor of the root node is greater than the root. All the values greater than the root node exist in its right subtree. Therefore, the Inorder Successor of the root node will always be in the right subtree.
The Inorder Successor is the smallest node among those greater than the root node. And the smallest node in the right subtree is the leftmost node. A node that has no left child is the smallest node in the right subtree (or we can say the leftmost node in the right subtree is considered the smallest node in that subtree).
To find the Inorder Successor node of any node, we can create a function where we pass the node whose Inorder Successor we want to find with a simple logic:
Node* IS(Node* root) {
// Pass the right child of the root node whose Inorder Successor we are searching
while (root->left != NULL) {
root = root->left;
}
return root;
}
This covers the first part of finding the Inorder Successor in a BST.
The second major point to remember about the Inorder Successor is that the node identified as the Inorder Successor will always have either 0 or 1 right child attached to it. Before moving further, we should ask: Can a node with 2 children be an Inorder Successor?
The answer is No. A node with 2 children cannot be the Inorder Successor because, by definition, the Inorder Successor is the leftmost node in the right subtree. If a node has a left child, it cannot qualify as the leftmost node of the right subtree.
Using Inorder Successor in Deletion:
After finding the Inorder Successor, we replace the root node with the value of the Inorder Successor. Once the replacement is done, we delete the Inorder Successor node from the tree. This way, we ensure the BST properties are maintained while deleting a node with two children.
#include<iostream>
#include<vector>
using namespace std;
class Node {
public:
int data;
Node* left;
Node* right;
Node(int value) {
this->data = value;
this->left = this->right = NULL;
}
};
void preorder(Node* root) {
if(root == NULL) return;
cout<<root->data<<" ";
preorder(root->left);
preorder(root->right);
return;
}
Node* insert(Node* root, int &value) {
if(root == NULL) return root = new Node(value);
if(value > root->data) root->right = insert(root->right, value);
else root->left = insert(root->left, value);
return root;
}
Node* buildBST(vector<int> &vec) {
Node* root = NULL;
for(int i=0; i<vec.size(); i++){
root = insert(root, vec[i]);
}
return root;
}
Node* inorderSuccessor(Node* root) {
while(root->left != NULL) {
root = root->left;
}
return root;
}
int main() {
vector<int> vec = {5, 1, 3, 4, 2, 7};
Node* root = buildBST(vec);
cout<<root->data<<endl;
preorder(root);
cout<<endl;
Node* ans = inorderSuccessor(root);
cout<<ans->data;
cout<<endl;
return 0;
}
/**
* Before deleting a node from the BST we first need to find the presence of that node im the BST.
* Once we reach at the node whose value we have to delete we just implement the 3 cases for deleting the node.
*/
#include<iostream>
#include<vector>
using namespace std;
class Node {
public:
int data;
Node* left;
Node* right;
Node(int value) {
this->data = value;
this->left = this->right = NULL;
}
};
Node* insert(Node* root, int &value) {
if(root == NULL) return root = new Node(value);
if(value < root->data) root->left = insert(root->left, value);
else root->right = insert(root->right, value);
return root;
}
Node* buildBST(vector<int> &vec) {
Node* root = NULL;
for(int i=0; i<vec.size(); i++) {
root = insert(root, vec[i]);
}
return root;
}
void inorder(Node* root) {
if(root == NULL) return;
inorder(root->left);
cout<<root->data<<" ";
inorder(root->right);
}
Node* inorderSuccessor(Node* root) {
while(root->left != NULL) root = root->left;
return root; //Inorder successor.
}
Node* deleteNode(Node* root, int deleteKey) {
if(root == NULL) return NULL;
//STEP-1: Searching Phase
//If the deleting node is less then the root node then we have to find it in the left subtree. And this will return us the updated left value of the root.
if(deleteKey < root->data) root->left = deleteNode(root->left, deleteKey);
else if(deleteKey > root->data) root->right = deleteNode(root->right, deleteKey); //If deleting root is more then the root node then we have to find the deleting node in the right subtree. And this will return us the updated right value of the root.
else {
//STEP-2: Here we have to handle the three cases of deleting a node in the BST
//Inside else part we are standing on the node which we want to delete.
//CASE 1: Deleting node having 0 child node.
if(root->left == NULL && root->right == NULL){ //So its a leaf node
delete(root);
return NULL;
}
//CASE 2: Having 1 child node either on the left or right side.
if(root->left == NULL || root->right == NULL) { //If any of the root left or right is NULL then we have to return the one which has valid value in it.
return (root->left == NULL) ? root->right : root->left;
}
//CASE 3: Having both 2 child node of the deleting node.
//We don't need any such if condition for case 3 because if the root was of 0 or 1 child node then it would have returned from the above two cases if its reaching till here then this means its the case of case 3.
//First thing in case 3 is getting the inorder successor of the root. For that we will pass the root->right value because in that only we need to find out the left most value in the right subtree.
Node* IS = inorderSuccessor(root->right);
//Replacing the root data with the inorderSuccessor data.
root->data = IS->data;
//And then finally we will call the deleteNode for our Inorder successor.
root->right = deleteNode(root->right, IS->data); //Here we have to make sure that we don't pass our root node as we have stored the IS data in the root too therefore passing the root here will make a infinite loop
//as root will have 2 children therefore we pass the root->right here as the root node to delete the next node from the root->right subtree.
return root;
}
return root; //If the value to be deleted doesn't exsits in the BST in that case we just need to return back the original root without any changes in it.
}
int main() {
vector<int> vec = {8, 5, 3, 1, 4, 6, 10, 11, 14};
Node* root = buildBST(vec);
inorder(root);
cout<<endl;
deleteNode(root, 15);
inorder(root);
cout<<endl;
return 0;
}
.
.
.
.
Lukewarm regards
Aman Pratap Singh